Archivo de la etiqueta: juego

Multiplicación y división de números decimales. Cuadrado mágico

Actividad que demanda tener asimilada la relación entre las operaciones multiplicación y división, aplicadas al caso de los números decimales

(pulsa sobre la imagen)

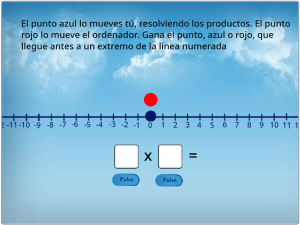
Producto de números enteros. Juego contra el ordenador

Deja un comentario

Juego de competición, para practicar el producto de números enteros. Se juega contra el ordenador. El punto azul se mueve de acuerdo con nuestras respuestas. El punto rojo lo mueve el ordenador.

(pulsa sobre la imagen)

Juegos de multiplicaciones, con dados

Deja un comentario

Proponemos los siguientes juegos de multiplicaciones, con dados.

Juego Juego Juego Juego Juego Juego Juego Juego

Ayudan a memorizar las tablas de multiplicar, pero de una manera más abierta, más lúdica. Son fácilmente extensibles a un formato manipulativo.

Pirámide de enteros

Deja un comentario

Interesante actividad, que demanda razonar y sumar números enteros

(pulsa sobre la imagen)

Múltiplos de 5. Juego de movimiento

Deja un comentario

Mostramos aquí el siguiente juego de múltiplos, que metodológicamente etiquetamos como un juego de movimiento

(pulsa sobre la imagen)

Juego con el sistema de numeración decimal

Deja un comentario

Nos parece conveniente introducir conceptos matemáticos mediante juegos y actividades lúdicas. También nos parece útil relacionar las situaciones de juego con actividades de la vida cotidiana. Por eso hemos planteado esta actividad, relativa al sistema de numeración decimal, que introducimos en el 5º curso de Educación Primaria: