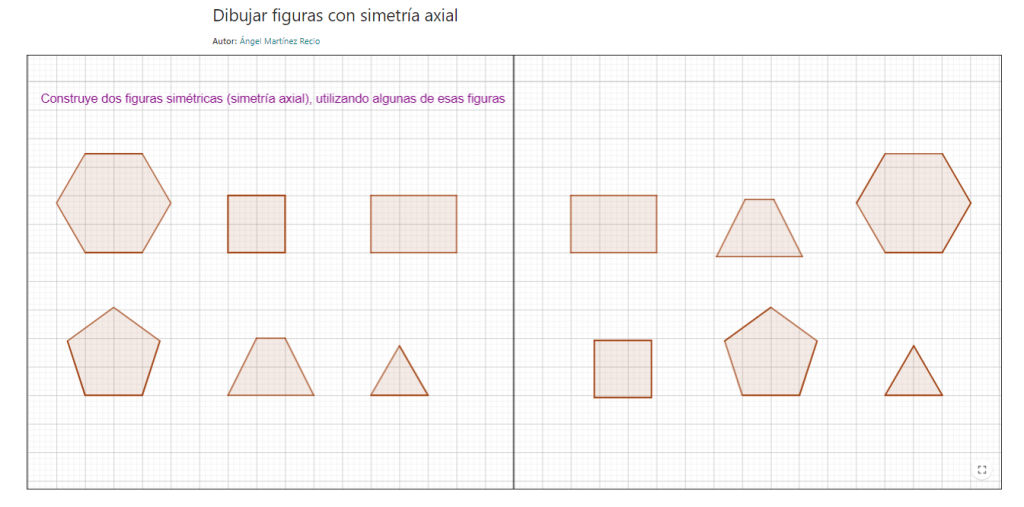
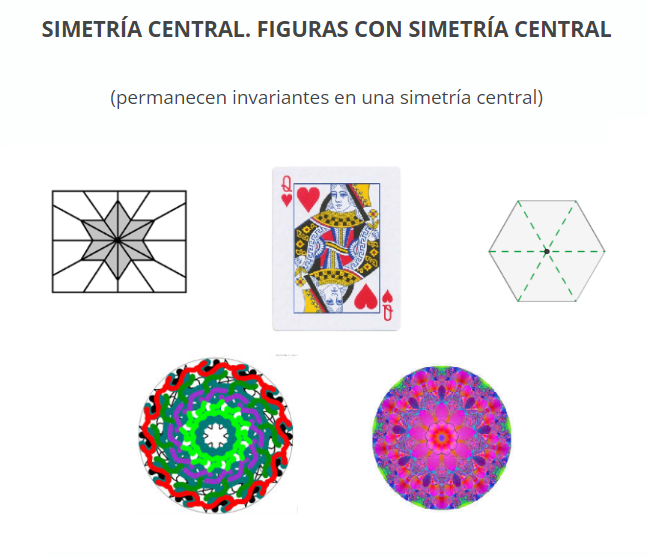
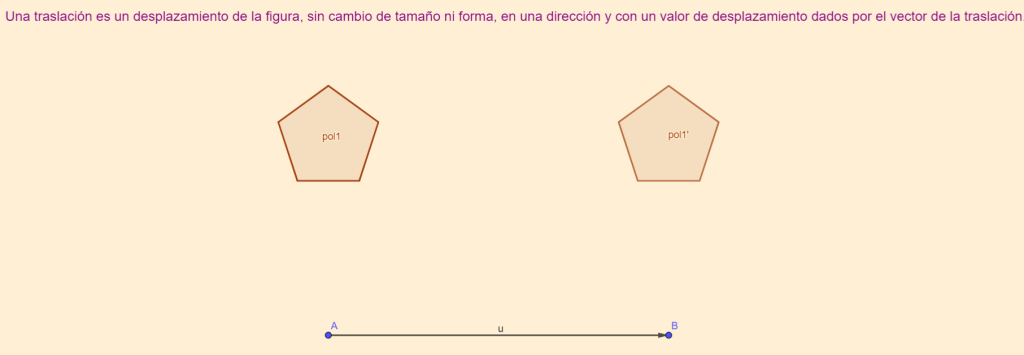
Consideremos el siguiente conjunto de problemas, tomados de una clase de 4º de ESO:

¿Para qué debemos enseñar este tipo de ejercicios?
Como deciamos en nuestra entrada anterior, estos alumnos de 4º de Eso, orientados a la opción de Ciencias, están desarrollando el pensamiento lógico deductivo, un tipo de pensamiento que es muy importante para alumnos de Ciencias y que estos problemas contribuyen a desarrollar.
Nuestra objeción es que estos ejercicios plantean unos tipos de cálculos demasiado alejados de la vida real y que pueden ser excesivamente artificiosos. Personalmente nosotros creemos que puede ser una alternativa más interesante la introducción en clase de Matemáticas del pensamiento informático , buscando igualmente al desarrollo del pensamiento deductivo.
En particular, creemos que la introducción a los alumnos en el mundo de GeoGebra, para ayudarles a comprender la forma de resolver estos tipos de problemas (aunque eligiendo problemas más simplificados), puede resultar bastante más instructivo.
Por ejemplo, puede ser más interesante enseñarles a explicar, mediante GeoGebra, la resolución de problemas tales como los que se consideran en:
https://www.geogebra.org/classic/tEN8HGKR
Es una clase de actividades que les obliga a comprender la forma de resolver las ecuaciones radicales, los pasos básicos a dar para resolver ecuaciones radicales, que es lo que en definitiva se pretende con los mismos. Se comprenden mejor esos métodos de resolución y además se aprende a programar en el mundo de Geogebra, programa estrictamente matemático, uno de los mejores programas informáticos a conocer por los estudiantes de estas edades.